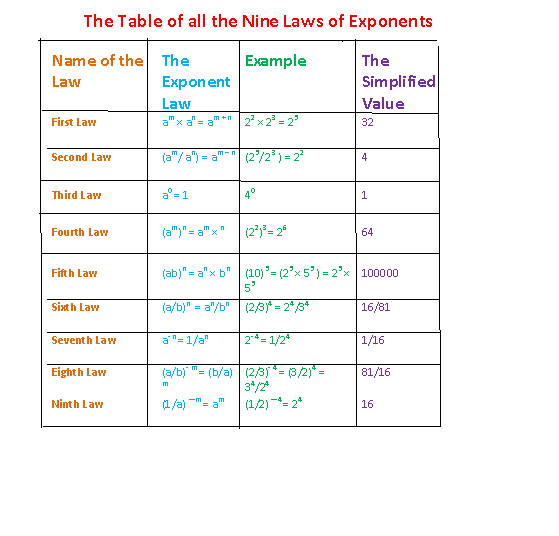
Laws of Exponents:

Let a be any number except 0 and m and n be two natural numbers. Then,

First Law of Exponents:
a^m × aⁿ = a ^{m + n}

Example 1:
3² × 3³ = 3^{2 + 3} = 3⁵ = 243

Example 2:
2⁴ × 2⁴ = 2⁸ = 256

Second Law of Exponents:
a^m / aⁿ = a^{m – n}

Example:
3⁶/3² = 3^{6 – 2} = 3⁴ = 81

Third Law of Exponents:
If a is any number except 0, then
a⁰ = 1.

Example 1:
5⁰ = 1
x⁰ = 1, if x is any number except 0.

Example 2:
9³/9³ = 9^{3 – 3} = 9⁰ = 1

Fourth Law of Exponents:
(a^m) ⁿ = (a)^{m × n}

Example 1:
(2²)³ = (2)^{2 × 3} = 2 ⁶ = 64

Fifth Law of Exponents:
(ab)^m = a^m × b^m

Example 1:
(10)⁵ = (2 × 5)⁵ = 2⁵ × 5⁵

Sixth Law of Exponents:
(a /b) ^m = a^m/b^m

Example:
(3/5)³ = 3³ / 5³ = 27/125

Very Important rules on exponents:
1. (a) ^?m = 1/a^m

Example:
(2) ^?4 = 1/2⁴ = 1/16

2. (1/a) ^?m = 1/ (1/a) ^m = a^m
Example:
(1/3) ⁴ = 3⁴

3. (a/b)^{- m} = (b/a) ^m
Example:
(2/3)^?4 = (3/2)⁴ = 3⁴/2⁴ = 81/16

4. (a^m) ^1/n = (a^m/n )
Example:
(2⁶)^1/3 = (2^{6 ×1/3}) = 2^6×1/3 = 2² = 4

nth root of a number Or A Surd:
Let a be a positive number and n a positive integer.
Then the nth root of a is denoted as:
nva or (a) ^1/n
a^1/n is called a Surd of order n.

Examples:
1. the 2^nd root of 25 is denoted as ²√25.
And (25)^1/2 = (5²)^1/2 = 5^2×1/2 = 5^2×1/2 = 5
2. the 3^rd root of 27 is ³√27
And (27)^1/3 = (27)^1/3 = (3³)^1/3 = 3^3×1/3 = 3^3×1/3 = 3
3. The 4^th root of 16 is ⁴√16
And ⁴√16 = (16)^1/4 = (2⁴)^1/4 = 2^4×1/4 = 2^4×1/4 = 2
4. The m^th root of a^m is ^m√a^m = (a^m)^1/m = a^m×1/m = a

nth root of a negative number:
Let a be a negative number, then the nth root of a will exist only if n is a positive odd integer, not when n is a positive even integer.

Example:
1. 3^rd root of -8 is ³√-8
And ³√-8 = (-8)^1/3 = (-2³)^1/3 = (-2) ^3×1/3 = 2^3×1/3 = 2
But, 2^nd root of -4 does not exist, since 2 is an even integer and if the exponent is even the base can’t be negative.

Note:
nth root of a positive number “a” is not defined in real numbers if n is an even integer, but
nth root of the positive number “a” exists in the set of complex numbers even if n is an even integer.
The Table summarizes all the laws of exponents.