Properties of Triangles
Before we take up the several properties of a triangle, typical and subject-oriented, we will, at the outset, encapsulate the more general and common ones that occur to an untrained mind, without portraying much the attending interest, labour and the need of a math student.
Here they go-
A triangle is a figure of three sides and three angles. More precisely, it is a polygon.
A triangle is a closed figure formed by joining any three non-collinear points (points that do not lie on a same straight line). Another derived way of conceiving a triangle is the figure formed by the intersection of three different straight lines.
A triangle has six elements or parts. They are the three sides or arms and the three angles.
A side of a triangle is formed by joining any two points. A side is therefore a straight line.
Therefore, a side is length of the line segment joining any two points or distance between the two points.
Since a side is a concept of length or distance, therefore it is measured in units which are applied for length or distance. And the units are centimetres, meters and such others.
Any two sides intersect at a point. The point is called a vertex. Thus, the three straight lines that a triangle is made of intersect at three different points.
An angle is formed by the intersection of two straight lines. Thus, the three angles in a triangle are formed by the intersection of the three sides at three different points.
The points of intersection of the sides are called Vertices. Therefore, a triangle has three vertices. Normally, the three vertices of a triangle are denoted by capital letters such as A, B, C or X, Y, Z or P, Q, R or any other triplets of letters written in capitals.
The space within the sides of a triangle is its interior region; outside of the sides is the exterior region and points on the triangle constitute the very triangle itself.
Triangles have areas and perimeter. Area is the total space contained inside the triangle which sum of the lengths of the three sides is the perimeter of the triangle.
The three sides and the three angles may be of equal lengths and measures or different.
Triangles are classified based on two factors. One is side, and the other is angle.
As said earlier, an angle is formed when the two sides of a triangle intersect each other at a point, called the vertex.
Angles are measured in degrees, radians and grades.
There are three major types of triangles classified under each of sides and angles.
Under the heading sides, the three major triangles are: Scalene, Isosceles and Equilateral.
Under angles, they are: Acute angled triangle, right-angled and obtuse-angled.
In a scalene triangle, all of the three sides are of different lengths, in isosceles, any two sides are equal and in the third type equilateral triangle, all the three arms/sides are of equal lengths.
In an acute angled triangle, all of the three angles are of different measures and every angle is less than 90 degrees.
A triangle in which one angle is 90 degrees is called a right-angled triangle. A right angle is denoted by placing a small square symbol at the vertex where it is formed. The side opposite of the right angle is called Hypotenuse. It is the longest side in a right-angled triangle. The two sides that contain the right angle are called legs of a right-angled triangle.
The celebrated pythagorean theorem applies on a right-angled triangle.
A triangle in which one angle is obtuse, i.e. greater than 90 degrees is called an obtuse- angled triangle. The side opposite to the obtuse angle is longest in the triangle.
In a triangle, angles and sides respectively opposite to each other are proportionately related. In other words, sides opposite equal angles are equal in lengths. And, the side opposite greater angle is longer than that opposite a smaller measure of angle.
The sum of the angles in a triangle is equal to 180 degrees.
With this overview, now let us delve into the specific properties in greater depth, the kind required for a math student.
Property 1:
Sum of the angles in a triangle is 180 degrees
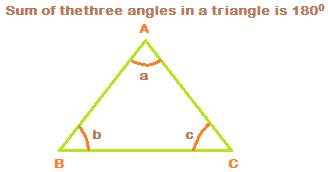
In the above triangle ABC, denoted as
, A, B and C are the three vertices formed by the intersection of the three sides AB, BC and AC.
The three angles 
are formed at the three vertices by the three sides AB, AC and BC.
is formed at vertex A, the point of intersection of the two sides AB and AC.
is formed at vertex B, the point of intersection of the two sides AB and BC.
is formed at vertex C, the point of intersection of the two sides AC and BC.
Now,
Property 2:
Exterior angle of a triangle
The exterior angle of a triangle is equal to the sum of the two opposite interior angles.
In the above
, one side BC is extended upto point D. Because of this, an angle is formed at vertex C from outside. This is called exterior angle. In the figure above, it is
. It is denoted as x.
Now,
Note that angles c and x form a linear pair of angles. Therefore,
c + x = 1800, so c = 1800 – x............1
but c = 1800 – (a + b)................2
from 1 and 2, we can write
1800 – x = 1800 – (a + b),
So, 1800 – x = 1800 – (a + b),
So, – x = – (a + b),
Therefore, x = (a + b)
Property 3:
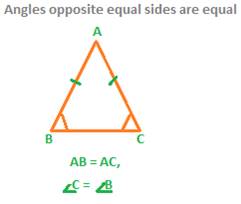
Angles opposite sides of equal and different lengths.
If two sides are equal in a triangle, then the angles opposite them are also equal. Conversely, if two angles are equal, then the sides opposite them are also equal.
Again, the side opposite the greater angle is longer than the side opposite a smaller angle.
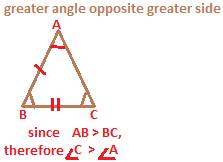
In the above figure, Side AB is longer than the side BC.
Now, opposite side BC it is angle A and opposite side AB it is angle C.
Since AB > BC, therefore angle C > angle A
Property 4:
Triangle Inequality of Sides
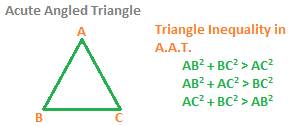
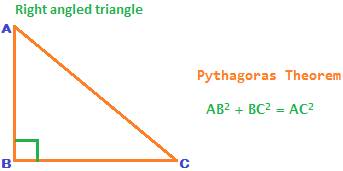
pythagorean Theorem:
The square of the length of hypotenuse is equal to the sum of the squares of the lengths of two sides containing the right angle.
AB2 + BC2 = AC2
