Parallel and Perpendicular Lines

Two straight lines are related to each other in four different ways. The two lines could be:

1. Parallel to each other


2. Perpendicular to each other


3. Intersect each other or


4. Skew lines.

Parallel Lines

Two lines that do not intersect each other are parallel to each other.

In the figure below, the two straight lines K and L are parallel to each other.

Denotation of Parallel Lines

The symbol // denotes parallel lines. Parallel lines do not intersect each other. Produce parallel lines infinitely at both directions of each line, still the two lines will never meet each other at any point.

The denotation K // L stands for “the two straight lines K and L are parallel to each other”.

In short, K is parallel to L.

Distance between Parallel lines

The distance between any two lines is the length of the straight line perpendicular to both the lines.

In the following figure, straight lines L1 and L2 are parallel to each other, i.e. L1 // L2

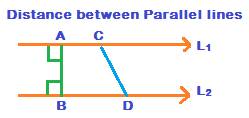
AB is the straight line perpendicular to both L1 and L2. CD is another line passing through the two lines L1 and L2 at two different points on them respectively.

CD is not perpendicular to any of L1 and L2

The distance between any two straight lines is always the shortest distance between them. And, the length of the line perpendicular to both the straight lines is the shortest distance. Therefore, AB is the distance between L1 and L2.

Note:

1. The straight line CD which is not perpendicular to one of the two lines or both is not taken as a distance between L1 and L2.
Distance between parallel lines is same everywhere

If two lines are parallel, then the perpendicular distance between any two points on the two lines is same.

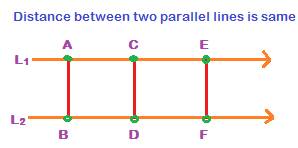
In the above figure, all of the three lines AB, CD and EF are perpendicular to both the lines L1 and L2. Therefore, the length of any of the three lines is distance between the parallel lines L1 and L2

Transversal:

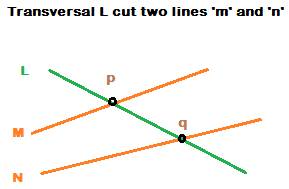
A line that cuts two or more lines is called a transversal.

In the figure above, Line ‘L’ is a transversal which cuts two other lines ‘M’ and ‘N’ at two different points ‘p’ and ‘q’ respectively.

Angles formed by parallel lines cut by a transversal

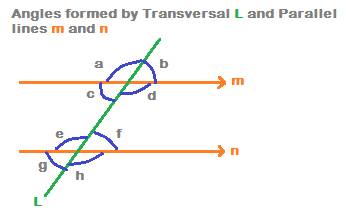
In the above figure, lines ‘m’ and ‘n’ are parallel to each other. Line ‘L’ is transversal that cuts the two lines m and n.

When a transversal cuts two lines which are parallel, then 8 angles are formed.

In the above figure, the eight angles formed by the transversal L that cuts parallel lines m and n are:

The 8 angles are divided into three major types. They are

• Alternate angles,
• Corresponding angles and
• Interior angles.

In the figure, the two pairs of alternate angles are c, f and d, e.

1. Since alternate angles are equal, therefore,

 and

2. the Four pairs of corresponding angles which are formed are again equal.

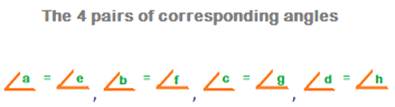
3. The Four interior angles which are formed are angles c, d, e and f.

Two lines parallel to a common line are parallel to each other too.

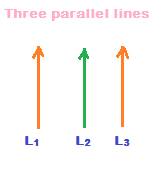
In the above figure, each of the two lines L1 and L3 is parallel to a common line L2.

i.e., L1 // L2   and L2 // L3. Then, L1 // L3

i.e., the two lines L1 and L3 are parallel to each other too.

Transitive Property of Parallel Lines

If L1 // L2,

and L2 // L3 , then

L1 // L3

Perpendicular Lines:

If the angle between two straight lines at the point of intersection is 900, then the two lines are perpendicular to each other.

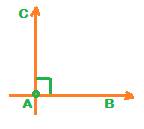
In the above figure, the two straight lines AB and AC are perpendicular to each other, as denoted by the small square symbol at point A.

A is the point of intersection of the two straight lines. The angle at point A is 900.

The small square symbol denotes 900.

Symbol for perpendicularity:

Two straight lines L1 and L2 perpendicular to each other are denoted as

L1 L2

Two lines perpendicular to a common line

Two straight lines perpendicular to a common line are parallel to each other.

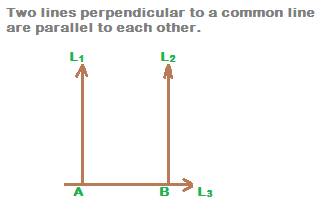
In the above figure, two straight lines L1 and L2 are perpendicular to a common line L3. Then they are parallel to each other.

If L1  L3, and

L2   L3, then

L1 // L2