Simple Interest and Compound Interest

What is Simple Interest?

It is the same interest added to principal for every year.

How much interest will an amount of $1000 deposited in a bank at 4% rate of interest per annum will generate?

Answer:

(1000 × 4 × 1)/100 = 40

$40 is the interest for 1 year.

$80 is the interest for 2 years.

Under simple interest method, interest is calculated on the sum of money, called principal, invested at the beginning.

Amount = Principal + Interest

So, in the above example, amount for

1 year is 1000 + 40 = 1040,

2 years is 1000 + 80 = 1080 and so on. 

The formula for finding simple interest on Principal P, for a time period T and at R% rate of interest per annum is:

Compound Interest:

Interest can be added to principal in another method.

It is added to the principal, the sum of money invested at the beginning,

The $40 interest can be added to the principal $1000 to yield the amount $1040.

If interest at 4% p.a. for 2nd year is calculated on $1040, instead of $1000, then interest is said to be added under compound interest method.

Compounding is adding interest to principal at regular accepted intervals of time.

Let Principal, P = $100, Time, T = 3 years, R = 10% p.a.

The following will illustrate the method of adding interest under the C.I. method:

Amount 110 is the principal for the 2nd year,

Amount 121 is the principal for the 3rd year,

Amount 133.1 is the principal for the 4th year.

Under compound interest, Amount is found by the formula given below:

 

The above formula is applied when compounding is done yearly, i.e. interest is added to principal at the end of every year for the whole duration of investment.

But, interest could be added to principal more frequently than at the end of every year.

Interest can be added half-yearly, quarterly, monthly also, under which the formula for finding the amount is as given below:

 

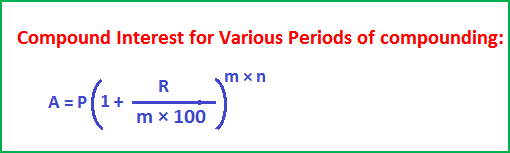
In the above formula, m stands for frequency of compounding:

If compounding is done:

Yearly, then m = 1,

Half-yearly, then m = 2,

Quarterly, then m = 4, and  Monthly, then m = 12