Slope of a straight line:

 

One of the properties of a straight line is slope.

Let a straight line pass through two points A (x1, y1) and B(x2, y2)

Then, the formula for finding slope of the straight line is

Slope is denoted by the letter ‘m’.

Note1:

x1, y1 are the coordinates of one point and x2, y2 are the coordinates of another point. Beyond this notation, no special significance is attached to the coordinates of the points in respect of sequence of points.

It appears from the subscripts used for the coordinates that there is a first point and a second point. But, this is purely a misgiving. You do not have to assume of any such convention.

The coordinates of any point serve to be taken as x1, y1 and those of the other as x2, y2.

Note 2:

The value of slope does not change even if the formula were written as follows:

But, there is a caveat. And it is

Do not reverse the order in the difference of x and y coordinates

Find difference of y coordinates and x coordinates in the same order.

After finding difference of y coordinate in one point to that in the second, do not make the mistake of finding the difference of x coordinate in the second to that in the first point.

In simple words, do not make the following mistake in finding slope:

Consider two points A (3, 6) and B (6, 9).

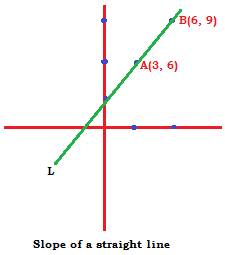
What is the slope of the straight line L passing through the two points A (3, 6) and B (6, 9)?

Applying the above formula, the slope is

Alternatively, the slope can also be found as

 

Warning:

Do not write different orders for the differences of x and y coordinates as below

  Or  

Consider the following general form of equation of a straight line

The slope of this straight line is

Example

Consider the straight line whose equation is

2x – 3y + 4 = 0

This equation is said to be in general form.

Therefore, its slope is

Trigonometric definition of slope

Consider the following figure.

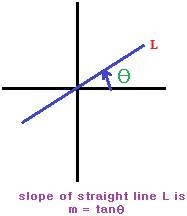
In the figure, the straight line L makes an angle θ with the positive direction of x-axis. The angle is counted anticlockwise from the x-axis to the straight line.

Then, slope of the straight line is tanθ