Triangles and Parts of Triangles

What is a triangle?

If three non-collinear points are joined by a straight line, then the closed figure formed is called a triangle.

In the above figure, the three points A, B and C are not collinear, i.e. do not lie on a same straight line.

The figure formed after the three points are joined by a straight line looks like the above one, a Triangle.

A triangle is a closed figure.

The three straight lines AB, AC and BC are called sides or arms of the triangle. So, a triangle has 3 sides all of which are 3 different straight lines.

A triangle is denoted by the symbol

A triangle formed by three non collinear points A, B and C is denoted as

The three points A, B and C of are called Vertices.

Also, a triangle has three angles, formed at the three vertices A, B and C.

The three angles at the three vertices A, B and C are denoted as

   

The three sides and three angles of a triangle are called parts or elements of a triangle.

Regions inside and outside of a triangle

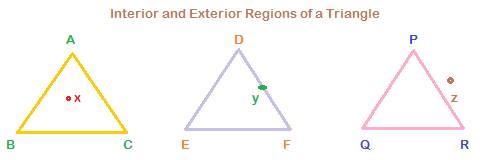
There are three regions with respect to a triangle:

Interior of, On and Exterior to a triangle.

Interior of a triangle:

In , point x lies inside the triangle. All of the space within the three sides AB, AC and BC form the interior region of the triangle.

On the triangle:

In , point y lies on the side DF, or the triangle DEF.

Exterior to a triangle:

For, point z lies outside. We say point z is in a region exterior to

Properties of angles in a triangle:

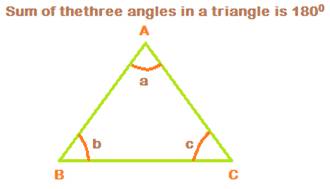
Take a, b and c to denote the three angles at the vertices A, B and C. Then,

a + b + c = 1800.

The angle sum property in a triangle is

2. The Exterior angle is equal to sum of the two opposite interior angles of a triangle

Consider the following triangle ABC.

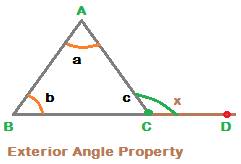
Extend side BC upto point D.

Then an angle at vertex C is formed. It is angle ACD.

This angle ACD is called exterior angle for triangle ABC.

Let x denote angle ACD.

And let a, b, c denote

From angle sum property

i.e. a + b + c = 1800, so c = 1800 – (a + b)

But

  form a linear pair of angles.

Therefore, c + x = 1800

So, c = 1800 – x

But, c = 1800 – (a + b)

Therefore, 1800 – x = 1800 – (a + b), so that we can write

x = a + b