Factorial of n, n!

1. What is Factorial of a number n, denoted as n!?

Factorial of any number n is denoted as n!

Factorial of a number is the product of all the positive integers from 1 up to

n, (including n) (n >= 1)

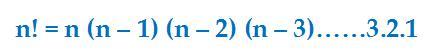
For example:



A Useful Tip:

Use the tip to simplify:



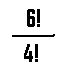
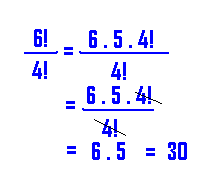
Let us now define n! (Factorial of a number n)

Consider

Now, what does 24 signify?

Without allowing any letter to repeat, 24 permutations (arrangements) can be formed taking all 4 different things at a time

Caught the point? No? Then Read on

How many ways can you seat four men a, b, c, d in four chairs?

Treat the four chairs as the blanks below:

----- ----- ----- -----

Any one of 4 persons can sit in the first chair; any 3 in the 2^nd; any 2 in the 3^rd; and 1 in the last chair

Filling each chair with a man is one task. And, there are four tasks here.

From rule of counting, the four tasks can be completed in 4.3.2.1 ways, i.e.,
24.

Each of the 24 ways is an arrangement or more popularly a permutation
To aid your understanding, listed below are the


So, what does 4! signify?
4! stands for 24 arrangements.
Another way to define 4! is
Without allowing things to repeat, the number of ways of arranging 4
different things is 4!.
Generalize 4!. How? As follows:

Definition of n!

Without allowing things to repeat, taking all in each permutation, n different things can be arranged in n! ways.
Note: 0! = 1

Solved Examples:

1. Use factorial formula to simplify:

Solution: in the given example write

10!-8!/8!-7!=8!(10.9-1)/7!(8-1)=8.7!(89)/7!.7=8.7!(89)/7!.7=89/7

2. Express 6.7.8.9.10 in factorial notation

Solution:

10.9.8.7.6=10.8.9.7.6.5.4.3.2.1/5.4.3.2.1=10!/5!