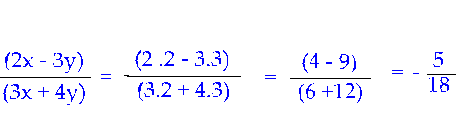The Letters are called variables and the numbers before them are called coefficients.

1. Letters used as symbols for numbers:

In the algebraic expression 2x, the letter x stands as a symbol for any number. One can choose any number to write for x . So, x holds a place for any number. One can write 3, 10, 100 or any other number as required for x . Since x changes or varies based on what is to be written for it, it is therefore called Variable.

What varies is a variable.

Other variables in the above examples for algebraic expression are p, q and y

2. Symbols used to denote Multiplication

1. Now consider 2x.

What does it mean? It means multiplication of 2 and x, i.e., 2 × x.

2 × x is also called product of 2 and x. Product refers to multiplication.

In 2x we know x is the variable and we also know it stands as a symbol to write any number for it. In other words, it holds a place to write any number for it.

Then let us see what will 2x become, when numbers like 3, 10, 100 are written for x

2x means product (multiplication) of 2 and x. So, we get
2 × 3 = 6, 2 × 10 =20, 2×100 =200

2. Again consider 2x

It may also be written as 2.x standing for multiplication (product) of 2 and x.

so, we have 2.x = 2.3 = 6 or 2.10 = 20 or 2.100 = 200, depending on what number is written for x.

In algebraic expressions, dot indicates multiplication

3. Consider 2x once again.

It can also be written as 2(x) standing for multiplication of 2 and x

So, we have 2(3) = 6 or 2(10) = 20 or 2(100) =200, based on what number we choose to write for x

Let us summarize the above three ways of representing multiplication in the table below:

Symbols used to denote Multiplication in Algebraic Expression

Consider examples to understand the three forms of Algebric Expression:

1. A dot placed between symbols

2.x = 2x, x.y = xy, 7.p = 7p and other examples

2. A parentheses between symbols or numbers

2(x) = 2x, x(y) = xy, 7(p) = 7p

3. Writing no operation sign between symbols (not numbers)

2x means 2×y
xy means x×y
7p means 7×p

Important Note:

Number 50 does not stand for product of 5 and 0 i.e., it is not 0, it is just the number 50. Only in Algebraic Expressions symbols like x and y not connected by any operation sign stand for multiplication of x and y.
----------------------------------------------------------------------------------------------------------------

3. Symbols used to denote Division

To denote division of x and y, we write x÷y. The algebraic expression x / y also stands for division of x by y

4. Converting Words into Symbols

5. Use of Parentheses

1. To stand for multiplication:

2(x) means 2 × x, i.e. the product of 2 and x
2(3) = 2 × 3 = 6
x (y) = x × y

2. To consider an Algebraic Expression as one number

3(p + q) is one number i.e., the product of 3 and sum of x and y

6. The Substitution Method:

It’s a very important method. It’s the basic method to find values of variables which stand as place holders. Let us see it below:

Find the value of each of the following algebraic expressions if x = 2 and y = 3

1. x + y

Solution:

just plug in 2 for x and 3 for y and called this substitution.
x + y = 2 + 3 = 5

2. 3x + 4y

Solution:

as in 1. above, just plug in 2 for x and 3 for y
3.2 + 4.3 = 6 + 12 = 18
(recall that 3x stands for multiplication of 3 and x and so also 4y)

3. (2x – 3y)/(3x + 4y)

Solution:

again as in 1 and 2 above, write the given values in x and y