Math-for-all-Grades.com
Lesson No. 1: Definition of Probability
Example 1:
Solution: Suppose you flip a coin.
What is the chance Heads will appear?
50% (i.e. 1/2)
What is the chance that tails will appear?
50% (i.e. 1/2)
Example 2:
Toss a dice. What is the probability that an even number will appear?
Solution:
The six numbers on a dice are 1, 2, 3, 4, 5, 6.
On the dice, 2, 4 and 6 are the even numbers.
So, the probability an even number will fall is 3/6 i.e. ½
Example 3:
In a bag, there are 3 green and 4 red marbles. Take out any two marbles out of the bag. What is the probability the two marbles are green-colored?
Solution: Bag contains 7 marbles. 2 marbles are taken out. 2 out of 7 can be taken out in 7c2 ways i.e. 21 ways.
(Recall that r things can be selected out of n things in ncr ways from combinations)
2 green out of 3 green marbles can be taken out in 3c2 ways i.e. 3 ways.
The probability is therefore: 3/21 = 1/7
From the three examples above, we can define probability as follows:
If E denotes an event, then the probability Event E will happen is:
P (E) = (Outcomes favorable for E)/ (Total number of outcomes)
The table below summarizes the salient points in the 3 examples above.

So, try a definition for Probability? Here we go:
Let E denote an Event and P (E) the probability that Event E will happen. Then,
P (E) = (Number of outcomes favorable for E)/(Total number of outcomes)
Five coins are tossed. Find the probability of:
1. 3 heads
2. At least 3 heads.
3. At most 2 heads.
4. 3 heads, exactly next to each other.
Solution: Use the above formula:
P (E) = (Number of outcomes favorable for E)/(Total number of outcomes)
First find the total number of outcomes when 5 coins are tossed.
It is 2 × 2 × 2 × 2 × 2 × 2 = 25 = 32 outcomes and not 2 × 5 = 10 outcomes.
(If 3 coins are tossed, the total number of outcomes is 2 × 2 × 2 = 8 outcomes and not
2 × 3 = 6 outcomes.)How, as follows:
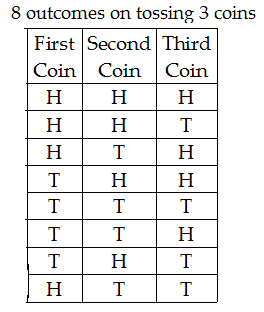
So, 3 coins give 2 × 2 × 2 = 23 = 8 outcomes.
Likewise, 5 coins give 2 × 2 × 2 × 2 × 2 = 25 = 32 outcomes.
Now, how many outcomes show 3 heads out of 32?
5c3 i.e. 10 outcomes. How? As follows:
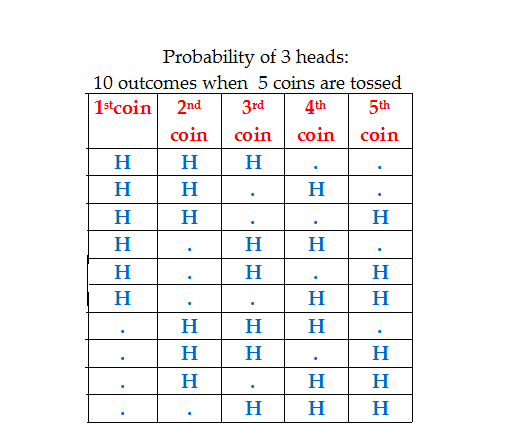
The dots indicate Tails.
Tabulating is difficult.
You must use an easier way to find favorable outcomes, with a formula probably.
And it is combinations formula: ncr
We need 3 Heads. Which 3 coins must show the required 3 Heads?
Any 3 coins. So, select any 3 coins out of the 5 coins. In how many ways?
Yes, in ncr ways, i.e. 5c3 ways i.e. 10 ways. Each way is one outcome, 10 ways are 10 outcomes.
So, the probability 3 Heads will appear is = 10/32 = 5/16
2. Probability of at least 3 Heads:
At least 3 heads means minimum 3 heads i.e.
3 or more heads i.e. 3 or 4 or 5 heads.
So, find probability of the following events:
3 heads or 4 Heads or 5 Heads
So, P (At least 3 Heads) = P (3H) or P (4H) or P (5H)
(Remember one rule: Write + for Or when it needs to used and × for And)
So, P (At least 3 Heads) = P (3H) + P (4H) + P (5H)
= ( 5c3 + 5c4 + 5c5 )/32
= (10 + 5 + 1)/32
= 1/2
3. Probability of at most 2 Heads:
At most means maximum 2 heads i.e. up to 2 heads, i.e. less than or equal to 2 heads.
So, find probability of the following events:
2 Heads or 1 Heads or No Heads.
So, P (At most 2 Heads) = P (2H) + P (1H) + P (0H)
= ( 5c2 + 5c1 + 5c0 )/32
= (10 + 5 + 1)/32
= 1/2
4. Probability of exactly 3 Heads, next to each other.
| 1st coin | 2nd coin | 3rd coin | 4th coin | 5th coin |
|---|---|---|---|---|
| H | H | H | . | . |
| . | H | H | H | . |
| . | . | H | H | H |
Dots indicate tails.
We must tabulate the outcomes that give 3 Heads as it is a special case.
P (3 Heads, next to each other) = 3/32
(Note: In the first row, 5th coin cannot show a Heads, for we need only 3 Heads and the series 5th, 1st and 2nd coin is not acceptable for Heads to fall next to each other).




