5. Important rule on change of base in logarithms:

Remember the following important rule related to change of base in logarithms

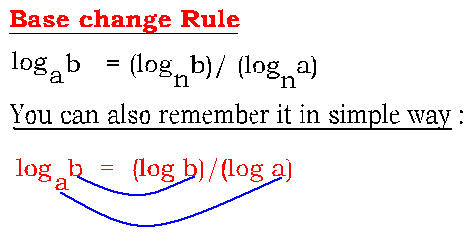
for example:
log ₆ 7 = (log ₅ 7)/(log ₅ 6)

6. Rule of Base Change

How to change base of logarithms:

log _a n = log _b n . log _a b

Without going into the proof and derivation of the rule, let us see this rule in a simple way taking the help of the formula:

log _a b = (log b)/(log a)

log _b n . log _a b

= [(log n)/(log b)].[(log b)/(log a)]

= log _a n

So, log _a n = log _b n . log _a b

Let us now solve a few problems based on the rule no. 3 and rule no. 4 on Base Change

1. Prove the following

1. log ₆₄ 3 = (log ₄ 3)/₃
2. log _pq a = (log _p a)/(1 + log _p q)

Solution1:

We will convert all logs into base 4, as we see log to base 4 in the right side in question no.

1. So,
log ₆₄ 3 = (log ₄ 3)/(log ₄ 64)

from Law 3 on laws of logarithms, we have

log _a (p)ⁿ = n log _a p

so, log ₄ 4 ³ = 3log 4⁴

= 3 . 1 = 3, since log ₄4 = 1

Therefore, (log ₄ 3)/ (log ₄ 64)

Solution 2:

we will convert all the logs into base p as we see base p on the right side.

log _pq a = (log _p a)/(log _p pq)

Now, log _p pq = log _p p + log _p q

= 1 + log _p q

Therefore,

log _pq a = (log _p a)/ (1 + log _p q)

7. Common Logarithms:

Logarithms expressed or calculated to base 10 are called Common Logarithms

For eg, log ₁₀ 5, log ₁₀ p are examples of

common logarithms.

Common logarithms such as log ₁₀ x, log ₁₀a

can also be merely expressed as log x or log a implying that the base 10 is understood and therefore need not be shown.

This holds only for logarithms to base 10.

For logarithms to any base other than 10, the base must be clearly mentioned. For example, if the base is 5, then it should be clearly mentioned as log₅ x.