Logarithm and Exponential Form of a Number

1. Definition of Logarithm:
Let a (≠1) and n be positive numbers and x be any real number. Then,
If ax = n,
then the logarithm of number n is written as
log a n = x
Consider the following examples to become clear of logarithms:

Exponential and Logarithm form


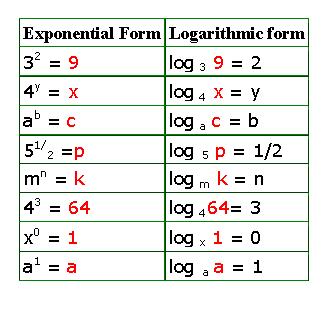
In each of the left cells above, the number ‘n’ whose logarithm is written in the right cell is written in red.
Definition of Logarithm:
The logarithm of a number n to a base a is x, where the number n is equal to a raised to the power x.
If ax = n, then
log a n = x
Observe the following results from the above table:

1. the logarithm of 1 to any base is 0
Because if loga 1 = x , ………………………………(1)
then 1 = ax , and from laws of exponents, we know that
if ax = 1, then x = 0
putting x = 0 in (1), we get
log a 1 = 0

2. the logarithm of any number to itself is 1.
because, if log a a = x,
then a = ax , so x = 1
therefore, log a a = 1

3. logarithm of only positive numbers exists.
Note: Logarithm of a number can be negative, but logarithm of a negative number does not exist.
For example,
log 3 (1/3) = log 3 3-1
= -1(log 33)
= -1(1) = -1
But log 3(-3) does not exist.
Therefore, in each of the left cells in the above table, the number in red is always positive.Let us now solve a few problems applying the logarithm formulas and concepts learned so far.


Top
Next Lesson - Problems on Logarithms