How to calculate area
In this page, we will discuss special formulas and methods for:
How to calculate area of:
- A triangle, when the length of its three sides are given
- A square, when the length of its diagonal is given
- A rectangle, the lengths of whose diagonal and perimeter are given
Question:
How to calculate area of a triangle if the lengths of its three sides are given?
Answer:
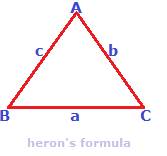
Use heron’s formula to calculate area of a triangle when the lengths of its three sides are given.
And, Heron’s formula is
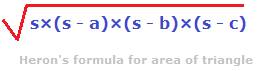
In the formula, a, b and c denote the lengths of the three sides of the triangle; and s is the semi-perimeter of the triangle, i.e.
s = (a+ b + c)/2
For example, the area of a triangle in which the lengths of the three sides are 6, 8 and 10 is
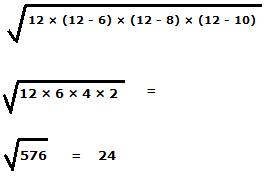
How to calculate area of a square when its diagonal length is given?
To calculate area of a square using its diagonal, the formula is
![]()
The area of a square whose diagonal length is 10 cms is
102/2 = 100/2 = 50 sq. cms.
How to calculate area of a rectangle whose perimeter and diagonal lengths are given?

In a rectangle, if length is l and breadth is b, then
Perimeter of the rectangle = 2 (l + b) and
Diagonal length = √(l2 + b2)
Apply the algebraic identity below, to calculate area of the rectangle:
(l + b)2 = l2 + b2 + 2lb,
Transpose l2 + b2 to the other side, so
2lb = (l + b)2 – ( l2 + b2),
Next divide by 2 to finally calculate area of the rectangle as below:
l× b = ((l + b)2 – (l2 + b2))/2
Related Topics


