Y-intercept
What is y intercept?
In this lesson, we will try to understand what is meant by y intercept?
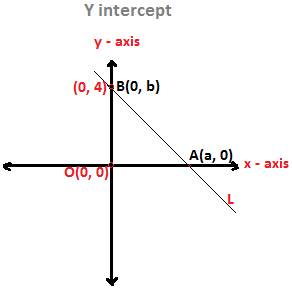
In the above XY Coordinate plane, consider a straight line L.
This line L passes through the point (a, 0) on the x-axis and the point (0, b) on the y-axis.
y intercept definition:
The y coordinate in the point (0, b) on the y-axis through which the line L passes is called the y intercept.
y intercepts exist with respect to a line. They do not exist independently.
i.e. the y coordinate of a point through which no straight line is given to pass does not turn into y intercept, rather it remains just as a y coordinate.
In the above figure, the straight line L passes through the point B (0, b) on the y-axis.
Therefore, the y coordinate b is the y intercept of the line L.
Since the y intercept is basically y coordinate, so it can be both positive and negative.
When the straight line passes through the y-axis from above the origin, then the y intercept is positive, because, y coordinates of points lying on y-axis above the origin are positive.
And again, the y intercept of the line that cuts the y-axis from below the origin is negative, because y coordinates of points lying below the origin are negative.
Thus, y intercepts are both positive and negative.
Now, we will discuss two methods below for finding y intercept of a line L
The following two methods for finding y intercept of a Line L will apply when the slope of the line and a point through which it is passing through are given.
Method-1:
Find the y intercept of a straight line L whose slope is 2 and which passes through the point P (3, 4)
Solution:
Recall from above, what is a y intercept?
It is the y coordinate in the point on the y-axis through which a line L will pass.
So, write the point as B (0, b), in which the y intercept of the Line L is b. Remember, this line L will pass through the point B (0, b).
Now, there are two points B (0, b) and P (3, 4) through which the Line will pass.
Again, slope of Line L is 2, as given.
Applying slope formula on B (0, b) and P (3, 4), we have,
(b – 4)/ (0 – 3) = 2,
b – 4 = -6, b = -6 + 4 = - 2
Method 2:
Alternatively, use equation of a straight line to find y intercept of a line L.
We can use the slope-intercept form of the equation of a straight line L, as since slope and a point through which the line is passing are given.
Now, the equation of a straight line L in slope-intercept form is
y = mx + b,
In this formula, m is slope of the line L and b is the y intercept.
Substitute the coordinates of the point P (3, 4) in the equation of the Line L as it is passing through this point and 2 in slope m.
4 = 2 × 3 + b,
So, b = - 2




