Collinear points

Collinear points definition:

Three or more points that lie on a same straight line are called collinear points.

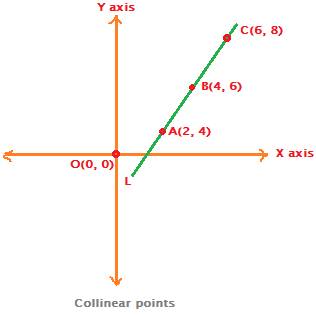
Consider a straight line L in the above Cartesian coordinate plane formed by x axis and y axis.

This straight line L is passing through three points A, B and C whose coordinates are (2, 4), (4, 6) and (6, 8) respectively.

{We may also say, alternatively, that the three points A (2, 4), B (4, 6) and C (6, 8)are lying on a same straight line L}

Three or more points which lie on a same straight line are called collinear points.

How to find if three points are collinear

There are two methods to find if three points are collinear.

One is slope formula method and the other is area of triangle method.

Slope formula method to find that points are collinear.

Three or more points are collinear, if slope of any two pairs of points is same.

With three points A, B and C, three pairs of points can be formed, they are:

AB, BC and AC.

If

Slope of AB = slope of BC = slope of AC,

then A, B and C are collinear points.

Example

Show that the three points A (2, 4), B (4, 6) and C (6, 8) are collinear.

Solution:

If the three points A (2, 4), B (4, 6) and C (6, 8) are collinear, then
slopes of any two pairs of points will be equal.

Now, apply slope formula to find the slopes of the respective pairs of points:

Slope of AB = (6 – 4)/ (4 – 2) = 1,

Slope of BC = (8 – 6)/ (6 – 4) = 1, and

Slope of AC = (8 – 4) /(6 – 2) = 1

Since slopes of any two pairs out of three pairs of points are same, this proves that A, B and C are collinear points.

Area of triangle to find if three points are collinear.

Three points are collinear if the value of area of triangle formed by the three points is zero.

Apply the coordinates of the given three points in the area of triangle formula. If the result for area is zero, then the given points are said to be collinear.

First of all, recall the formula for area of a triangle formed by three points.

It is

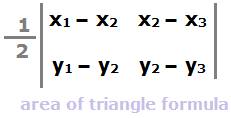
In the formula above, the two vertical bars enclosing the variables represent a determinant.

Let us apply the coordinates of the above three points A, B and C in the determinant formula above for area of a triangle to check if the answer is zero.

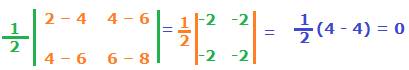
Since the result for area of triangle is zero, therefore

A (2, 4), B (4, 6) and C (6, 8) are collinear points.