Math-for-all-Grades.com
Permutations and Combination
What you will learn in this lesson on Permutations and Combinations?
Tell me in how many ways you (A) and your brother (B) can sit in two chairs before the TV?
2 ways, right?
AB and BA.
Now, you (a), your dad (b) and your mom (c) can sit in three chairs in how many ways?
Hmm, interesting but thoughtful!
Here it is:
abc, acb, bac, bca, cab, cba.
First, you occupy the first chair. Ask your dad and mom to exchange the other two seats in two ways.
Now, its your dad’s turn in the first chair. Now, you and mom will exchange the other two chairs in two ways.
Last, your mom will lead. Like to exchange seats with your dad in two ways? Try it anyway!
So, how many?
Six, in all.
Made it? Yes, you did!
Now, face this. More stuff to dig your brains deep
What if your teeth-grinder brother (d) joins in?
Hmm, big trouble? But, no escape!
You must let in your parents’ other half.
See how many ways you, your brother, your dad and your mom can sit in four chairs?
Here goes the list of

How many totally? My god! 24. That’s too many. Right? Ok.
Now I won’t ask you to add your friend Joe too.
Each of the above 24 sequences is called a permutation.
Permutations are also called arrangements.
We say 4 different persons denoted by letters a, b, c and d can be arranged in 24 ways.
We use a formula to find this. Including the formula, we learn other numerous cases in which the formula will be applied to produce various other formulas
If you wish to set off with your lesson on Permutations and Combinations, then click on the link below:
Permutations and Combinations
Or, if you wish to capture a terse overview of each Permutations and Combinations Formula, then go through each of the following header-links. You can also click the header-links to take you to the page on the specific Permutations and Combinations formula:
Fundamental Rule of Counting:
If there are m ways of doing one task, and n ways of doing another task, then the two tasks can be done one after other in m × n ways.
Factorial of n,n!
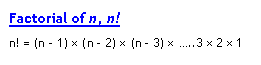
the number of ways in which n different things can be arranged by taking all at a time, when each thing can appear only once in every arrangement is called Factorial of n, denoted as n!
Each of the arrangements represented by n! is called a permutation.
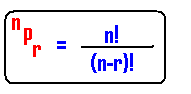
Again each of the npr arrangements is also called a Permutation.

the number of ways in which n different things can be arranged (permuted) by taking r at a time, when each thing is allowed to repeat any number of times (upto a maximum number of r times) is nr

Each of the arrangements is a permutation
The number of ways in which n different things can be arranged by taking all at a time, if p things are same of one type, q things are same of a second type and the remaining of the n things are all different from each other is

Note that every arrangement is a permutation.
Circulur Permutations
The number of ways in which n different things can be arranged around a circle is :(n – 1)!
Each of the arrangements around the circle is called a circular permutation.
Circular Permutations: Clockwise and Counter-clock wise
If the clock wise or anti-clock wise direction of permutations around a circle are not relevant, then the number of permutations around a circle is only
[(n – 1)!]/2.
Combinations:
Suppose you (A) and your brother (B) wish to team up to play badminton against a group of two of your friends.You and your bro can make how many teams?
Of course, only one team.
The team can be named as AB.
Will the team BA be different from the team AB?
You guessed it. It’s not!
Teams AB and BA are same, i.e., not different from each other. They are not different because the two members A and B, i.e. you and your brother are the same team members irrespective of whether the team is called AB or BA.
So, there we have a clear distinction between an arrangement and a group.
As a permutation AB and BA are different from each other, but as a group (combination) AB and BA are same.
ncr
From n different things, by taking any r things at a time, the number of groups that can be formed is ncr
A useful alternative definition of ncr
The number of ways in which any r things can be selected out of n different things is ncr
Important formulas on Combinations:
- nc0 = 1
- ncn = 1
- ncr = ncn-r
- The number of groups (combinations) of n different things taking any number at a time is:
nc0 + nc1 + nc2 +….. ncn = 2n – 1 - The number of ways (alternatively groups or combinations) in which n things can be divided into p things and q things is

- The number of ways (alternatively groups or combinations) in which 3n can be divided equally into three distinct groups each having n things is
- The number of ways (alternatively groups or combinations) in which 3n can be divided equally into three identical groups each having n things is