Math-for-all-Grades
Pythaogras Theorem
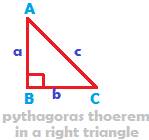
In a right angled triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides
(We do not intend to present here the proof of Pythagoras theorem, despite the fact that numerous proofs exist and the popularity that the proofs of this theorem enjoys. Rather, our aim is to apply Pythagoras theorem to solve a few questions- a practical point of view)
Written as an equation, the Pythagoras theorem is
AB2 + BC2 = AC2
i.e. a2 + b2 = c2
where a and b are the lengths of the two sides that contain the right angle, while c is the length of the side opposite the right angle.
The longest side in a right triangle is opposite of the right angle.
It is called hypotenuse.
The following right angled triangles are some examples illustrating the Pythagoras theorem:
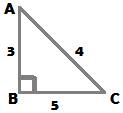
In triangle ABC, the Pythagoras theorem is
AB2 + BC2 = AC2
The lengths of the three sides AB, BC and AC are 3, 4 and 5.
Now, verify the Pythagoras theorem by applying the values in the theorem’s statement as below:
32 + 42 = 52
i.e. 9 + 16 = 25 which is a true statement.
Therefore, 3 and 4 are the legs of the right triangle, while 5 is hypotenuse length.
In the following table, some famous Pythagorean triplets are given
Legs of the Right triangle |
Hypotenuse Length |
Pythagorean Theorem |
6 and 8 |
10 |
62 + 82 = 102 |
5 and 12 |
13 |
52 + 122 = 132 |
7 and 24 |
25 |
72 + 242 = 252 |
Caution
If the lengths of two sides in a triangle are 3 and 4, it is not necessary that the third side must be 5 and therefore it is not necessary that a right triangle is definitely formed if two sides are 3 and 4. The third side need not necessarily be only 5. It can be any other number as the explanation below will clarify:
According to triangle inequality property of sides, in a triangle the length of any side should be less than the sum of the lengths of the other two sides in the triangle.
From this property, if ‘c’ is the length of the third side, then
c < 3 + 4, i.e. c < 7.
Any number less than 7 can be a value for c, the third side length, not necessarily 5.
But, if the lengths of the three sides of a triangle are 3, 4 and 5, then the triangle formed is certainly a right angled triangle; for,
32 + 42 = 52
Converse of Pythagoras Theorem:
If the square of the length of one side of a triangle is equal to the sum of the squares of the lengths of the other two sides, then the angle opposite the longest side is a right angle.
Or briefly put, it is
If the square of one side equals the sum of the squares of the two other sides, then a right angle is formed.
In the triangle ABC below, the lengths of the sides are 10, 8 and 6. Does the triangle have a right angle?
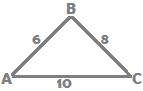
Answer:
Check Pythagoras theorem.
Is 102 = 62 + 82
Is 100 = 36 + 64?
Is 100 = 100?
Yes it is.
Therefore, a right angle is formed opposite the side of length 10
Two very important types of right angled triangle:
450–450-900 right angled triangle.
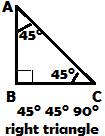
In the right angled triangle ABC above, the three angles are 450, 450 and 900.
If the length of the side
AB opposite 450 is x, and
BC opposite 450 is x, then
AC, the hypotenuse is of length x√2
300–600-900 right angled triangle
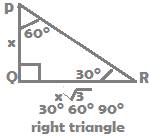
In the right angled triangle PQR above,
let the length of the side
PQ opposite 300 be x; then
QR opposite 600 will be of length x√3; and
Hypotenuse PR will be of length 2x.




