Points And Lines

Geometry basics

 Geo means earth and metry stands for measurement, so that geometry is measurement of earth; earth or parts of earth or still more objects in earth.
In this lesson we will consider some standard definitions which form foundations and conventions for more developed concepts in Geometry.

Point

A point is a location in space. (By the way space is where objects extend into)

In the figure below, the dots in various colours are Points.

How many points are there in the figure below?

Actually, several, countless, infinite points exist in space. But only four have been displayed (against the white background which is a plane. A plane exists in space too.S) in the figure with colours.

Where do you see the points located in?

Space!

In the figure below, X and Y in blue are two points displayed.

Where do you see the two points shown on?

On line AB

(Oh! by the way, what is a line? We will discuss it shortly below)

Curve:

In the following figure:

A and B are points at the two ends of the line AB.

The path from A to B through either of the points C or D is a curve.

ACB and ADB are two curves

It may be said ACB and ADB are curved paths or circular paths, while the path along the straight line AB is a linear path.

Note:

The length of line segment AB is also termed distance between the two points AB. And it is the straight line path AB that is the shortest distance between the two points A and B.

Line

A straight path indefinitely extending on two opposite directions is called a Line.

In the Line L in the figure below, the two opposite ends extend infinitely. Since we cannot represent indefinite extension of the two opposite ends of the Line L, the two ends appear terminated.

Note:

A line L does not have length as it extends in both the opposite directions infinitely.

A line is believed to have no breadth too.

Line Segment

A line joining two points, say A and B and running over all the points between A and B in a straight path is a Line segment.

The two points A and B are called the end points of the line segment AB.

Line segment AB is denoted with a line written above capital letters A and B, as shown in pink above.

Ray

A straight line with one end point at A and extending indefinitely beyond another end point B is called a Ray AB.

A ray joining two points AB is denoted with an arrow mark on AB.

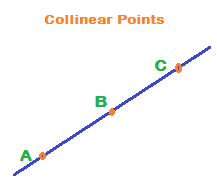
Collinear Points

Three or more points that lie on a same straight line are called collinear points.

The straight line passing through the points is called the line of collinearity.

 

Off the track Side Note:

Whether three points are collinear or not can be found in coordinate geometry using the following two methods:

1. Find slope of any two pairs of the three points. If it’s a same value, then the three points are collinear.

2. Apply the formula for area of triangle on the three points. The given three points are collinear if the answer for area is zero.

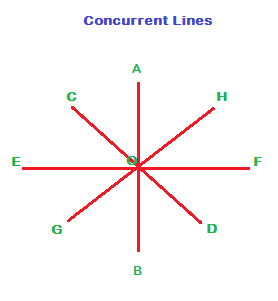
Concurrent Lines:

In the following figure, three straight lines AB, CD and EF intersect at the point ‘O’. Three or more straight that intersect at a point are called concurrent lines.

The point of intersection is called point of concurrence.

 

In the figure below, AB is a line segment.

The length of line segment AB is the distance between the two end points A and B. This distance is denoted as AB.

Mid-point

Like wise, if AM and BM are equal, i.e. if length of line segments AM and BM are equal, then M is said to be the Mid-point of the line segment AB.

The straight line PM is said to divide the line segment AB into two equal parts.

A line that divides another into two equal parts is called a bisector of the second line.

In the figure below, straight line PM is the bisector of the line segment AB.

Additionally, if line PM is perpendicular to AB, it is called perpendicular bisector of AB.

Two lines are perpendicular to each other, if the angle at the point of their intersection is 90 degrees.

Mid point and Line bisector

Note:

Two straight lines which are equal in length are denoted by same number of strokes marked on them.

In the above figure, the two line segments AM and BM are equal in length. Therefore, a stroke is marked on them showing that they have same length.