Math-for-all-Grades.com
Circular Permutation
Lesson no. 4: Circular Permutations:
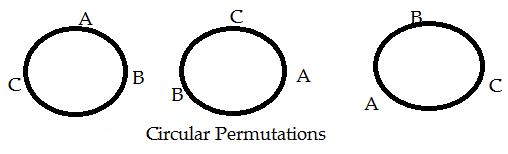
How can A, B, C be arranged around a circle?
Not in the three ways as shown above! Why?
Because each one of A, B, C has the same neighbor!
Without changing neighbor, only changing seats will not change the circular permutation.
Change neighbors and you will change the circular permutation. As follows:
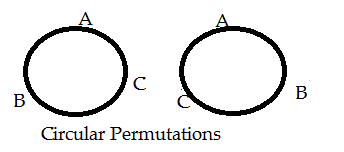
So, three persons A, B, C can only be arranged in 2 ways around a circle.
In a formula type it is:
Generalize. How? As follows?
n different things can be arranged around a circle in (n – 1)! ways.
In other words, with n different things, there are:

Clock wise and Anti-Clock wise permutations:
Consider the figure:

You thought the circular permutations change on changing neighbors.
Not really. Why?
Changing neighbors can change circular permutations only when you treat clock wise direction different from the anti-clock wise.
What if you treat the two directions same?
Then only one circular permutation!
Generalize. How? Like below:
Without treating the two directions differently, n different things can be arranged around a circle in many
 ways.
ways.



